Introducción.
En este Blog hablaremos sobre los temas de variable e Integración por partes. Se mostraran fotos, ejercicios y otras cosas más en la que te podrás apoyar para realizar sus trabajos.
Propósito
Tratamiento analítico de las integrales definidas e indefinidas y uso intuitivo de los procesos infinitos y las situaciones límite.
Cambio de variable.
Este método consiste en transformar la integral dada en otra más sencilla mediante un cambio de la variable independiente. El papel de cambio de variable en la integración es comparable al de la cadena en la derivación
El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
Queremos realizar la integral ∫ ƒ(x) dx donde ƒ no tiene una primitiva inmediata. Debemos buscar un cambio de variable que transforme la integral en una integral inmediata o composición de funciones. Entonces, para el cambio,
x = g(t)
dx = g′(t)dt
∫ ƒ(x) dx = ∫ f(g(t))g′(t) dt
De esta forma se ha transformado el integrando en función de la nueva variable t u otra letra. Si la elección de la variable t ha sido acertada, la integral resultante es más sencilla de integrar. El éxito de la integración depende, en grado considerable, de la habilidad para elegir la sustitución adecuada de la variable.
Una vez obtenida la función primitiva, F(t) + C, se deshace el cambio de la variable substituyendo t = g (x).
Ejemplo:1.-Determina ∫ (3x − 5)4 dx
Solución. En este caso sencillo podemos observar que esta integral "se parece" a
∫ u4 du, lo cual nos sugiere tomar el cambio de variable u = 3x-5.
u = 3x-5 ⇒ du = 3 dx ⇒ dx = (1/3)du
Sustituyendo en la integral,
∫(3 x − 5)4 dx ==∫u4 du / 3 = ⅓∫ u4 du
=⅓(u5/5 ) + c = u5/15 +c=∫(3 x − 5)5/15 +c
2.-Determina
En general, cuando tengamos una raíz en una integral, realizamos el cambio de variable con el contenido de la raíz o bien toda la raíz. En este caso, el cambio de variable es:
de donde podemos despejar la x:
Y en esta última expresión derivamos en ambos miembros:
(el cambio t=x-1 también es posible)
Como ves, una vez hecho el cambio de variable, tenemos que buscar la forma para poder poner todos los factores que aparecen en la integral en función de la nueva variable.
Ahora sustituimos los factores de la integral por los nuevos factores en función de x:
Operamos y sacamos fuera la constante:
Integramos aplicando el método de integrales inmediatas:
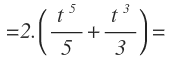
Operamos para eliminar el paréntesis:

Y finalmente, volvemos a cambiar la variable «t» por su expresión en función de x y le añadimos la constante:
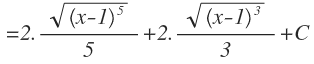
3.-Determina ∫sen
3
x · cos
4
x dx
Solucion. cos x=t → −sen x dx=dt → dx=
dt
−sen x
∫sen
3
x · cos
4
x dx=∫sen
3
x ·t
4 dt
−sen x
=∫−sen
2
x ·t
4
dt=∫(cos
2
x−1)·t
4
dt=∫(t
2−1)·t
4
dt
∫(t
6−t
4
)dt=
t
7
7
−
t
5
5
+C
deshacer cambio =cos
7
x
7
−
cos
5
x
5
+C
Links de apoyo:
https://sites.google.com/site/ittcalculointegrallogisticas2/ejercicios-resueltos---por-cambio-de-variable
https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/integracion-por-sustitucion-o-cambio-de-variable.html
https://ekuatio.com/integracion-por-sustitucion-o-cambio-de-variable-ejercicios-resueltos/
Links de apoyo:
https://sites.google.com/site/ittcalculointegrallogisticas2/ejercicios-resueltos---por-cambio-de-variable
https://www.superprof.es/apuntes/escolar/matematicas/calculo/integrales/integracion-por-sustitucion-o-cambio-de-variable.html
https://ekuatio.com/integracion-por-sustitucion-o-cambio-de-variable-ejercicios-resueltos/
Integración por partes
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
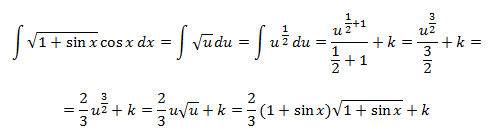
- Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU).
- Aunque se trata de un método simple, hay que aplicarlo correctamente.
- Método:
- El integrando debe ser un producto de dos factores.
- Uno de los factores será u y el otro será dv.
- Se calcula du derivando u y se calcula v integrando dv.
- Se aplica la fórmula.
- Escoger adecuadamente u y dv:
Una mala elección puede complicar más el integrando.
Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x3). Si consideramos dv = x3. Entonces, integrando tendremos que v = x4/4, con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.
Normalmente, se escogen los monomios como u para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.
Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv = 1/x, tendremos v = log|x| y, probablemente, obtendremos una integral más difícil.
Como norma general, llamaremos u a las potencias y logaritmos y dv a las exponenciales, fracciones y funciones trigonométricas. - No cambiar la elección:
A veces tenemos que aplicar el método más de una vez para calcular una misma integral.
En estas integrales, al aplicar el método por n-ésima vez, tenemos que llamar u al resultado du del paso anterior y dv al resultado v. Si no lo hacemos así, como escoger una opción u otra supone integrar o derivar, estaremos deshaciendo el paso anterior y no avanzaremos. - Integrales cíclicas:
En ocasiones, tras aplicar dos veces integración por partes, tenemos que despejar la propia integral de la igualdad obtenida para poder calcularla.
Ejemplos: 1.-Determina
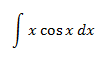
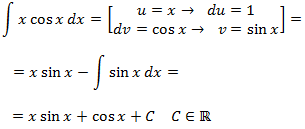
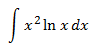
Nota: interesa escoger u = x2 (para reducir su exponente) pero entonces nos vemos obligados a que dv = ln(x) y obtener v no es inmediato. Así que escogemos lo contrario:
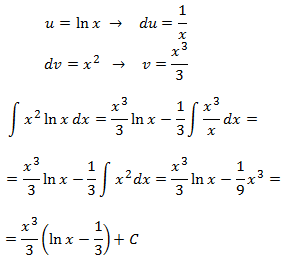
3.-Determina
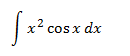
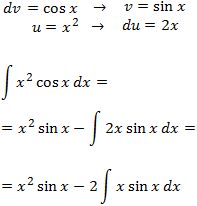
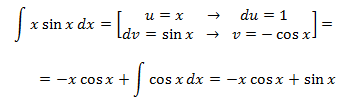
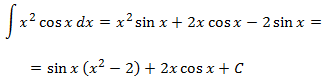
Links de apoyo:
Presentacion de power point

